Второй закон Кеплера — это одно из трех фундаментальных положений в сфере астрономии и планетологии, разработанных немецким астрономом Иоганном Кеплером в XVII веке. Этот закон, также известный как закон радиус-векторов, описывает движение планет вокруг Солнца и является ключевым элементом в формулировке современной астрономической механики.

Формула второго закона Кеплера выглядит следующим образом: площадь, заметаемая радиус-вектором от Солнца до планеты за определенное время, пропорциональна этому времени. Другими словами, скорость, с которой планета перемещается по своей орбите, изменяется в зависимости от ее положения относительно Солнца.

Такая интерпретация закона позволяет объяснить неравномерность движения планет по орбите: ближе к Солнцу, орбитальная скорость планеты выше, а на больших расстояниях — ниже. Это явление знаменито как «равномерное разности планет». Уравнение для второго закона Кеплера позволяет ученным оценить скорость движения планет в конкретные моменты времени и предсказывать их положение на орбите в будущем.

Описание второго закона Кеплера:

Второй закон Кеплера, также известный как закон равных площадей, утверждает, что за равные промежутки времени, проведенные линией, соединяющей Солнце и планету, площади, заметаемые этой линией, будут равны.

Это означает, что планеты двигаются по орбитам с переменной скоростью. Когда планета находится ближе к Солнцу, она движется быстрее, а когда находится дальше, она движется медленнее.

Геометрически, это можно представить с помощью эллипса, где Солнце находится в одном из фокусов. Линия, проведенная от Солнца к планете, заметает равные площади в равные промежутки времени при движении планеты вдоль орбиты.

Второй закон Кеплера является важным элементом для понимания движения планет вокруг Солнца. Он помогает установить связь между скоростью планеты и ее расстоянием от Солнца.

Планета	Скорость движения	Расстояние от Солнца
Меркурий	47,87 км/с	57,91 млн км
Венера	35,02 км/с	108,2 млн км
Земля	29,78 км/с	149,6 млн км
Марс	24,13 км/с	227,9 млн км

Краткое описание.

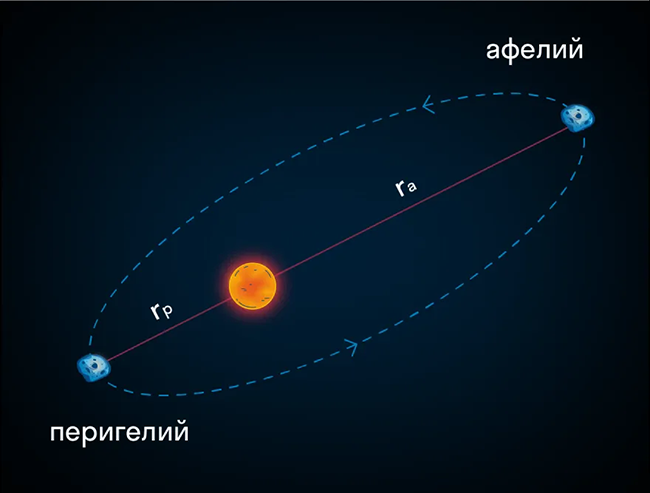
Этот закон позволяет понять, что скорость планеты изменяется в разные моменты ее орбиты, в зависимости от удаленности от Солнца. Ближе к Солнцу планета движется быстрее, а дальше – медленнее. Также, второй закон Кеплера объясняет, что планеты тратят больше времени на полный оборот в дальней точке своей орбиты – афелии, наибольшего удаления от Солнца, и меньше времени на полный оборот в ближней точке – перигелии, наименьшего удаления.

Формула для вычисления второго закона Кеплера представляет собой равенство:

r1^2 * t1 = r2^2 * t2,

где r1 и r2 – радиусы-векторы, связывающие Солнце с планетой в двух разных точках орбиты, а t1 и t2 – промежутки времени, за которые планета описывает соответствующие площади.

Второй закон Кеплера имеет широкое применение в астрономии и при изучении движения планет и других небесных тел. Он позволяет установить связь между скоростью планеты, ее положением на орбите и временем, затрачиваемым на обход Солнца.

Формула второго закона Кеплера.

Формула второго закона Кеплера, также известного как закон равных площадей, описывает скорость радиус-вектора, соединяющего планету с Солнцем, для каждой точки ее орбиты.

Согласно формуле второго закона Кеплера, векторная скорость планеты равна постоянной величине, умноженной на единичный вектор, перпендикулярный плоскости орбиты планеты и направленный в плоскости орбиты.

Математически формула выглядит следующим образом:

v = h / r

где:

• v — векторная скорость планеты;
• h — постоянная величина, равная площади, заметаемой радиус-вектором планеты за равные промежутки времени;
• r — длина радиус-вектора.

Формула второго закона Кеплера позволяет описать закономерности движения планет по орбите и объяснить, что в разных точках орбиты планеты она движется со скоростью, зависящей от расстояния до Солнца.

Интерпретация второго закона Кеплера:

Второй закон Кеплера, также известный как закон равных площадей, говорит о том, что радиус-вектор, соединяющий Солнце и планету, за равные промежутки времени описывает равные площади в плоскости орбиты. Этот закон позволяет понять, как планеты движутся вокруг Солнца и как их орбиты изменяются во времени.

Интерпретация второго закона Кеплера основывается на том, что равность площадей, описываемых радиус-вектором, означает равномерность скорости движения планеты в разные моменты времени. То есть, когда планета находится ближе к Солнцу, ее скорость увеличивается, а когда она находится дальше от Солнца, скорость уменьшается.

Это означает, что планеты орбитальные скорости не постоянны и зависят от расстояния до Солнца. Подобная зависимость позволяет объяснить, почему планеты двигаются со сменяющейся скоростью по орбите. Например, когда планета приближается к Солнцу, она движется быстрее, чтобы пройти большее расстояние за то же время, что и при более дальнем местоположении.

Этот закон также позволяет выразить связь между периодом обращения планеты вокруг Солнца и ее средним удалившемся от Солнца расстоянием. Чем больше у планеты среднее расстояние, тем дольше ей требуется времени на обращение вокруг Солнца. Это представление подкрепляет идею о том, что планеты двигаются по эллиптическим орбитам с Солнцем в одном из фокусов.

Историческое значение.

Согласно второму закону Кеплера, радиус-вектор, соединяющий Солнце и планету, сканирует равные площади за равные промежутки времени. Это означает, что планеты движутся быстрее во время своих перигелий (ближайших точек к Солнцу) и медленнее во время афелий (самых удаленных точек от Солнца).

Исторически значимым стало открытие Кеплером данного закона, поскольку он помог установить правильную картину движения планет в Солнечной системе. Ранее астрономы верили, что планеты движутся по круговым орбитам вокруг Солнца. Однако наблюдения Кеплера показали, что орбиты планет являются эллиптическими.

Открытие второго закона Кеплера было признано фундаментальным прорывом в астрономии и положило начало новому пониманию движения планет. Этот закон стал основой для развития теоретической астрономии и способствовал разработке более точных моделей орбитального движения планет.

В настоящее время второй закон Кеплера применяется в различных сферах научного исследования, включая астрономию, космическую навигацию, аэродинамику и ракетостроение. Историческое значение этого закона подчеркивается тем, что он помог установить фундаментальные принципы орбитального движения и открыл новые возможности для изучения вселенной.

Современная интерпретация.

Современная интерпретация второго закона Кеплера включает анализ общей теории относительности Альберта Эйнштейна и развитие космологии.

Согласно общей теории относительности, масса и энергия искривляют пространство-время вокруг себя, что в свою очередь оказывает влияние на движение объектов. Таким образом, планета, движущаяся по эллиптической орбите вокруг Солнца, искривляет пространство-время вокруг себя, и это искривление влияет на ее движение.

Кроме того, второй закон Кеплера также нашел свое применение в космологии. Изучая движение галактик и скоплений галактик, ученые обнаружили, что они также подчиняются законам Кеплера. В этом контексте второй закон Кеплера помогает исследователям понять распределение гравитационной массы внутри галактик и скоплений галактик.

Первое применение.

Первое применение второго закона Кеплера связано с определением орбит планеты. Закон утверждает, что радиус-вектор, проведенный от Солнца до планеты, заметает равные площади за равные промежутки времени. Это позволяет нам определить форму и размеры орбиты, а также расчетное положение планеты в пространстве.

Период времени	Радиус-вектор	Площадь
Т1	Р1	S1
Т2	Р2	S2
Т3	Р3	S3

С помощью таких данных можно не только определить параметры орбиты, но и предсказать будущее положение планеты в пространстве. Это имеет важное значение для космических миссий и интерпланетарных полетов, а также для понимания и изучения законов движения планетарных систем и вселенной в целом.

Влияние на современную науку.

Второй закон Кеплера сыграл важную роль в развитии науки и позволил сделать значительные открытия в области астрономии и физики. Используя этот закон, ученые смогли точно определить орбиты планет в солнечной системе и предсказать их движение. Это позволило осуществить множество космических миссий и исследований, включая посадку на Луну и отправку межпланетных зондов к другим планетам.

Второй закон Кеплера также стал основой для развития теории гравитации. Изучение движения планет и их соотношения с Солнцем позволило Исааку Ньютону сформулировать закон всемирного тяготения. Этот закон стал фундаментальным в физике и описывает движение всех небесных объектов, а также объектов на Земле.

Современная наука активно использует второй закон Кеплера для изучения и моделирования движения планет, комет и других небесных объектов. С его помощью ученые могут предсказывать будущее движение планет и проводить более точные наблюдения. Это помогает в изучении эволюции Солнечной системы и предсказывает возможное столкновение Земли с астероидами или кометами.

Применение	Описание
Космические миссии	Второй закон Кеплера позволяет спланировать исследовательские миссии, такие как отправка зондов к другим планетам или космических тел
Гравитационные исследования	Второй закон Кеплера позволяет изучать и моделировать гравитационные взаимодействия между небесными объектами и позволяет лучше понять структуру вселенной.
Космология	Использование второго закона Кеплера помогает ученым изучать эволюцию вселенной, предсказывать ее будущее развитие и понять ее возникновение.

Вопрос-ответ:

Как формулируется второй закон Кеплера?

Второй закон Кеплера формулируется так: радиус-вектор, проведенный из Солнца к планете, за равные промежутки времени всегда описывает одинаковые площади.

Как интерпретировать второй закон Кеплера?

Второй закон Кеплера означает, что планета движется быстрее, когда находится ближе к Солнцу, и медленнее — когда находится дальше от него. Это объясняется изменением скорости планеты в своей орбите, чтобы поддержать постоянное описываемое ею площадь.

Какая формула используется для вычисления площади, описываемой планетой вторым законом Кеплера?

Формула для вычисления площади, описываемой планетой, основанной на втором законе Кеплера, выглядит так: S = (1/2) * r^2 * dT, где S — площадь, r — радиус-вектор, проведенный к планете из Солнца, dT — промежуток времени.

Как можно применить второй закон Кеплера в реальной жизни?

Второй закон Кеплера может быть применен для определения скорости планеты в разных точках ее орбиты или для вычисления периода обращения планеты вокруг Солнца. Он также может быть использован для изучения движения спутников вокруг планет или искусственных спутников вокруг Земли.

Откуда у Кеплера появились данные для формулировки второго закона?

Данные для формулировки второго закона Кеплера были получены на основе наблюдений, проведенных Тихо Браге, который внес значительный вклад в изучение движения планет. Кеплер использовал эти наблюдения и свои собственные расчеты, чтобы сформулировать свои законы.