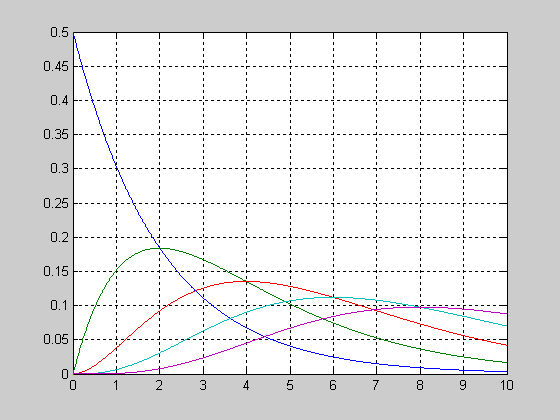
Закон Пуассона – это математический закон, которым описывается случайный процесс событий, происходящих независимо и с постоянной интенсивностью в некотором интервале времени или пространства. Он был введен французским математиком и физиком Симоном Дени Пуассоном в начале XIX века. Закон Пуассона широко применяется в различных областях, таких как вероятность, статистика, теория массового обслуживания и других.
Формула Пуассона позволяет рассчитать вероятность P(k) того, что в заданном интервале времени или пространства произойдет k событий. Формула выглядит следующим образом:
P(k) = (λ^k * e^(-λ)) / k!
где λ — среднее количество событий, происходящих за данный интервал, e — число Эйлера (приближенное значение 2.71828), k — количество событий.
Пример применения закона Пуассона может быть следующий. Предположим, что в среднем на дороге происходит 5 аварий в день. Мы можем использовать формулу Пуассона, чтобы рассчитать вероятность того, что в определенный день произойдет 3 аварии. Подставив значения в формулу, получим:
P(3) = (5^3 * e^(-5)) / 3! ≈ 0.14037
Таким образом, вероятность того, что в определенный день произойдет ровно 3 аварии, составляет примерно 0.14037 или 14.037%.
Определение и основные свойства
Данный закон формализуется математическим выражением, называемым формулой Пуассона. Формула представляет собой вероятностное распределение, которое позволяет рассчитать вероятность того, что в определенный промежуток времени или пространство произойдет заданное количество событий.
Основные свойства закона Пуассона:
- Фиксированная интенсивность — закон Пуассона описывает процессы, которые происходят с постоянной интенсивностью. Это означает, что среднее количество событий, происходящих за определенный период времени или пространство, остается постоянным.
- Независимые события — закон Пуассона предполагает, что каждое событие происходит независимо от других событий.
- Дискретность и непрерывность — закон Пуассона применяется как для дискретных, так и для непрерывных случайных величин.
- Суммируемость — закон Пуассона имеет свойство суммируемости, что означает, что если два процесса соответствуют закону Пуассона с разными параметрами, то их сумма также будет соответствовать закону Пуассона.
Закон Пуассона находит широкое применение в областях, где требуется моделирование случайных процессов с постоянной интенсивностью, таких как телекоммуникации, оценка риска и финансовая аналитика.
Понятие закона Пуассона
Закон Пуассона применяется для моделирования событий, которые происходят со случайными интервалами времени, таких как приход клиентов в магазин, количество телефонных звонков, поступление заказов и других подобных процессов. Он основан на следующих предположениях:
- События происходят независимо друг от друга.
- Средняя интенсивность событий постоянна в течение заданного временного периода.
- Вероятность возникновения события за очень малый интервал времени пропорциональна длине этого интервала.
Математически закон Пуассона описывается формулой:
где:
— вероятность того, что произойдет ровно k событий
— среднее количество событий в единице времени
— математическая константа, основание натурального логарифма
Таблицу с примерами применения закона Пуассона можно привести следующим образом:
| Пример | Количество событий (k) | Среднее количество событий (λ) | Вероятность (P(X=k)) |
|---|---|---|---|
| Поступление заказов | 0 | 1 | 0.3679 |
| Телефонные звонки | 2 | 3 | 0.2240 |
| Приход клиентов | 1 | 2 | 0.2707 |
Закон Пуассона играет важную роль в различных областях, таких как теория вероятностей и статистика, биология, экономика, телекоммуникации и другие. Он помогает предсказывать и описывать случайные события и является одним из фундаментальных инструментов для анализа случайных процессов.
Основные свойства закона Пуассона
Основные свойства закона Пуассона:
- Распределение Пуассона описывает события, которые происходят независимо друг от друга.
- События, которые случаются согласно закону Пуассона, не могут происходить одновременно (максимум одно событие на данный момент времени или в данной области пространства).
- Свойство возможности повторения событий дает возможность использовать закон Пуассона для моделирования процессов, где вероятность появления события мала, но общее число событий велико.
- Математическое ожидание и дисперсия закона Пуассона равны параметру λ, который представляет собой среднее число событий, происходящих за фиксированный промежуток времени или в заданной области пространства.
- Сумма независимых случайных величин, распределенных по закону Пуассона с одним и тем же параметром λ, также будет иметь распределение Пуассона с параметром, равным сумме λ для всех входящих случайных величин.
Закон Пуассона широко используется в различных областях, таких как телекоммуникации, физика элементарных частиц, экономика, биология и др. Он позволяет аппроксимировать сложные случайные процессы и предсказывать вероятность появления событий.
Формула и математическое описание закона Пуассона
Формула закона Пуассона выглядит следующим образом:
P(k) = (λ^k * e^(-λ)) / k!
где:
- P(k) — вероятность того, что произойдет событие ровно k раз;
- λ — среднее число событий, происходящих на протяжении заданного промежутка времени или в пространстве;
- e — основание натурального логарифма;
- k — количество событий, которое хотим предсказать.
Математическое описание закона Пуассона может быть применено в различных областях, таких как статистика, медицина, физика, экономика и других. Например, он может использоваться для оценки вероятности отказа технического оборудования, подсчета числа посетителей на сайте в определенный временной период, анализа распределения болезней в популяции и других случайных событий.
Формула Пуассона и ее особенности
Формула Пуассона имеет следующий вид:
P(k, \lambda) = \frac{e^{-\lambda} \cdot \lambda^{k}}{k!}
где:
- k – количество событий;
- \lambda – интенсивность событий;
- e – математическая константа, приближенное значение 2,71828;
- k! – факториал числа k.
Особенностью формулы Пуассона является возможность расчета вероятности наступления определенного количества событий, при условии, что интенсивность этих событий постоянна и события происходят независимо друг от друга. Формула также позволяет определить вероятность наступления отсутствия событий (когда k = 0).
Применение формулы Пуассона широко распространено в различных областях, таких как теория вероятностей, статистика, физика, биология, экономика и др. С ее помощью можно оценить вероятность наступления различных событий и принять обоснованные решения на основе полученных результатов.
Математическое описание закона Пуассона
Математически закон Пуассона формулируется следующим образом:
- События происходят независимо друг от друга.
- Вероятность того, что событие произойдет в заданный промежуток времени или пространства, постоянна и не зависит от предыдущих событий.
- Ожидаемое количество событий, которые произойдут в заданном промежутке времени или пространства, определяется интенсивностью событий.
- Распределение числа событий следует распределению Пуассона.
Математически закон Пуассона представлен формулой:
P(k; λ) = (λ^k * e^(-λ)) / k!,
где:
- P(k; λ) — вероятность того, что произойдет k событий в заданный промежуток времени или пространства;
- λ — интенсивность событий (среднее количество событий, происходящих в единицу времени или пространства);
- k — количество событий, которые произойдут в заданный промежуток времени или пространства;
- e — основание натурального логарифма;
- k! — факториал числа k.
Закон Пуассона имеет широкое применение в различных областях, таких как теория вероятностей, статистика, физика, экономика, телекоммуникации, биология, демография и другие. Он позволяет моделировать случайные процессы и предсказывать количество событий в заданный промежуток времени или пространства.
Примеры применения закона Пуассона
Пример 1: Анализ телефонных звонков
Компания телефонной связи проводит анализ длительности звонков, поступающих в их диспетчерский центр. Используя закон Пуассона, они могут предсказать, сколько звонков они получат в течение определенного временного периода. Эта информация помогает им эффективно планировать работу операторов и ресурсы центра.
Пример 2: Исследование трафика на дорогах
Государственное управление дорожным движением проводит исследование плотности трафика на определенных участках дороги. Они могут использовать закон Пуассона для предсказания количества автомобилей, проезжающих через определенную точку в течение определенного времени. Это помогает им принимать меры по улучшению трафика и планированию дорожных работ.
Пример 3: Анализ отказов в системе
Компания занимается разработкой программного обеспечения и они проводят анализ отказов в системе для улучшения качества своего продукта. Они используют закон Пуассона, чтобы определить среднее количество отказов, которые могут произойти в системе за определенный период времени. Эта информация помогает им предпринимать меры для устранения проблем и повышения надежности системы.
Это только некоторые примеры применения закона Пуассона. Он может быть использован во многих других областях, где требуется моделирование случайных событий. Знание этого закона позволяет прогнозировать и анализировать вероятности появления редких событий, что может быть полезным в различных сферах человеческой деятельности.
Пример применения закона Пуассона в теории вероятностей
Рассмотрим пример применения закона Пуассона в теории вероятностей. Представим, что в ресторане за час поступает в среднем 6 заявок на доставку еды. Мы хотим узнать вероятность того, что в следующем часу поступит 8 заявок.
Для решения данной задачи мы можем использовать формулу Пуассона:
P(x) = (e^-λ * λ^x) / x!,
где P(x) — вероятность поступления x заявок, λ — среднее количество поступающих заявок за заданный интервал времени, e — основание натурального логарифма, x! — факториал числа x.
В нашем примере среднее количество поступающих заявок за час равно 6. Подставляя значения в формулу Пуассона, мы можем вычислить вероятность появления 8 заявок:
P(8) = (2.71828^-6 * 6^8) / 8!
Вычислив данное выражение, мы получим вероятность появления 8 заявок в следующем часу.
Таким образом, использование закона Пуассона позволяет оценить вероятность появления заданного количества событий в заданном промежутке времени или пространства. Этот закон широко применяется в различных областях, таких как теория массового обслуживания, физика, экология, медицина и другие, где требуется анализ случайных процессов.
Пример применения закона Пуассона в статистике и экономике
Примером применения закона Пуассона в статистике является анализ числа аварий на дорогах за определенный период времени. Предположим, что мы хотим узнать, сколько аварий происходит в среднем за один час на определенном участке дороги. Мы можем использовать закон Пуассона, чтобы оценить вероятность определенного числа аварий в заданное время.
В экономике закон Пуассона может быть применен для анализа числа клиентов в очереди в банке или магазине. Представим, что у нас есть банковское отделение, в котором клиенты приходят на обслуживание в случайное время и с разной интенсивностью. Используя закон Пуассона, мы можем оценить, как часто возникают определенные длительности ожидания и сколько клиентов обычно находятся в очереди.
Закон Пуассона также может быть применен для анализа числа заявок, поступающих на сайт или веб-сервис, что может быть полезным для оптимизации серверных ресурсов или для планирования обработки данных.
Вопрос-ответ:
Что такое закон Пуассона?
Закон Пуассона — это математическое описание случайной величины, представляющей собой количество событий, происходящих в течение фиксированного временного интервала или на заданной площади. Он устанавливает вероятность появления конкретного числа событий при известной интенсивности.
Какая формула используется для вычисления вероятности по закону Пуассона?
Формула для вычисления вероятности по закону Пуассона имеет следующий вид: P(k) = (lambda^k * e^(-lambda)) / k!, где lambda — среднее количество событий за фиксированный интервал времени или площадь, k — конкретное число событий, e — математическая константа, а k! — факториал числа k.
Как закон Пуассона применяется в практических задачах?
Закон Пуассона широко применяется в различных областях, таких как теория вероятностей, статистика, физика, экономика и другие. Например, он может использоваться для моделирования случайных событий, таких как число звонков в колл-центре за определенный период времени, число аварий на дороге в течение суток или число просмотров видео на платформе в единицу времени.
Можете привести пример применения закона Пуассона в реальной жизни?
Конечно! Одним из примеров применения закона Пуассона может быть анализ количества аварий на дороге в течение определенного временного интервала. Предположим, что в среднем происходит 2 аварии в час. С помощью формулы Пуассона мы можем вычислить вероятность того, что за 3 часа произойдет ровно 5 аварий. Это может быть полезным, например, для планирования работ по ремонту и обслуживанию дороги.
Как можно математически описать закон Пуассона?
Закон Пуассона можно математически описать следующим образом: если случайная величина X соответствует числу событий, происходящих за фиксированный интервал времени или на заданной площади, то вероятность того, что X принимает значение k, равна P(X=k) = (lambda^k * e^(-lambda)) / k!, где lambda — среднее количество событий за интервал времени или площадь.
Что такое закон Пуассона?
Закон Пуассона — это математический закон, описывающий случайные события, которые происходят с постоянной интенсивностью в некотором интервале времени или пространства. Закон Пуассона определяет вероятность того, что определенное количество событий произойдет за определенный период.
Какая формула используется для расчета вероятности по закону Пуассона?
Формула Пуассона используется для расчета вероятности определенного количества событий, происходящих с постоянной интенсивностью в некотором интервале времени или пространства. Формула имеет вид: P(k) = (e^(-λ) * λ^k) / k!, где λ — среднее количество событий за определенный период, k — число событий, для которых мы хотим рассчитать вероятность, и e — основание натурального логарифма.